The Precision Horizon
A New Physical Law Governing Measurement Limits in the Cosmic Context
Abstract
This essay proposes a novel theoretical framework connecting statistical accuracy requirements to fundamental thermodynamic and cosmological constraints through the mathematical relationship σ_max = f(E_universe, k_B T, measurement_efficiency). We argue that the energy costs of observational precision scale exponentially with sigma confidence levels, creating an absolute "accuracy horizon" beyond which quantification becomes thermodynamically impossible within our observable universe. This synthesis of information theory, quantum thermodynamics, and cosmological physics reveals why the current scientific pursuit of extreme statistical confidence (beyond 7-sigma) may represent a fundamental dead end rather than a technical challenge to be overcome.
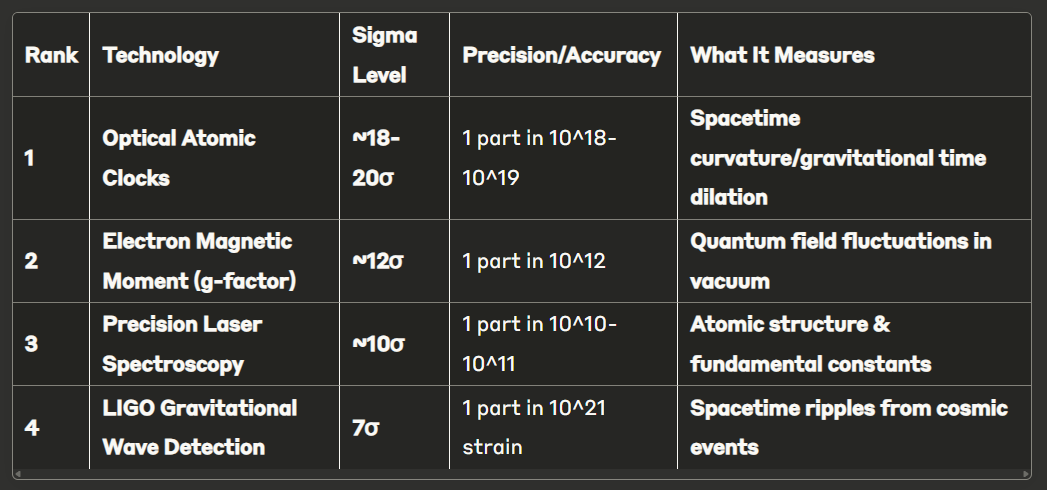
Most Precise Measurements of Reality's Fabric - Sigma Ranking
Key Insights:
Most Precise Overall: Atomic clocks can detect gravitational effects from moving just 30 cm higher on Earth - they're literally watching spacetime bend in real-time.
Different Types of "Fabric":
LIGO: Dynamic spacetime (waves)
Atomic Clocks: Static spacetime (curvature)
Electron g-factor: Quantum vacuum structure
Laser Spectroscopy: Fundamental constants of nature
The Paradox: LIGO has "only" 7σ confidence but measures the smallest displacements ever detected (10^-21), while atomic clocks achieve 18-20σ precision but measure larger effects (time dilation).
Note: Sigma levels represent different concepts - statistical significance for LIGO vs. measurement precision for others.
I. Introduction: The Convergence of Accuracy and Impossibility
Modern science has achieved extraordinary observational precision. The Laser Interferometer Gravitational-Wave Observatory (LIGO) can detect changes in distance smaller than 1/10,000th the width of a proton, representing perhaps the most exquisite quantification ever achieved by human beings. Yet this remarkable accuracy confronts a profound theoretical challenge when we consider the thermodynamic costs of information processing and the finite energy budget of our observable universe.
We propose what we term the Infinite Observation Paradox: that our most sophisticated scientific analyses, regardless of their local exactness, approach fundamental limits imposed by the intersection of information theory, quantum thermodynamics, and cosmic energy constraints. This paradox suggests the existence of a calculable "accuracy horizon" - a specific confidence level beyond which quantification becomes physically impossible.
Our central thesis: the scientific community's current pursuit of ever-higher statistical confidence represents a collision course with fundamental physical limits that have not been adequately recognized or quantified. We propose a new scaling law that makes these constraints explicit and calculable.
II. The Precision-Energy Scaling Law: A New Physical Relationship
The Proposed Mathematical Framework
We hypothesize that the maximum achievable statistical confidence in any observation is governed by the relationship:
σ_max = f(E_universe, k_B T, measurement_efficiency)
Where:
σ_max represents the maximum achievable sigma confidence level
E_universe is the total energy budget available for analysis (~10^69 joules for the observable universe)
k_B T represents the thermal energy scale of the observational environment
measurement_efficiency captures the technological and quantum mechanical limitations of the analytical apparatus
Theoretical Foundations
Several established principles support this relationship:
Landauer's Principle establishes that erasing one bit of information requires minimum energy dissipation of k_B T ln(2). Recent extensions by Latune & Elouard (2025) demonstrate that "the higher the quality, the larger the energy cost" for quantum observations, with precise mathematical bounds linking analytical fidelity to thermodynamic work requirements.
Lloyd's Cosmic Computational Limits provide the universal energy constraint. The observable universe can perform at most 10^120 elementary operations using approximately 10^69 joules. This finite computational capacity places absolute bounds on any information processing task, including high-accuracy quantification.
Quantum Fisher Information Framework rigorously connects observational exactness to "coherence costs" - the minimum energy needed to prepare distinguishable quantum states. This framework provides the theoretical bridge between statistical confidence levels and thermodynamic energy requirements.
The Exponential Scaling Hypothesis
Our central claim: the energy cost of achieving n-sigma confidence scales exponentially:
E_measurement ∝ exp(σ²)
This exponential relationship, absent from current literature, emerges from the compound effect of several factors:
Statistical requirements for higher confidence demand exponentially more data
Quantum coherence costs increase exponentially with analytical fidelity
Thermal noise suppression requires exponentially more energy at higher accuracy levels
Theoretical Example: The Escalating Energy Cascade
To illustrate this scaling relationship, consider a hypothetical accuracy analysis of a fundamental constant. Assume a baseline energy requirement E₀ for achieving 3-sigma confidence (99.7% confidence level).
At 3-sigma confidence: E = E₀ × exp(3²) = E₀ × exp(9) ≈ E₀ × 8,103 At 5-sigma confidence: E = E₀ × exp(5²) = E₀ × exp(25) ≈ E₀ × 7.2 × 10¹⁰ At 7-sigma confidence: E = E₀ × exp(7²) = E₀ × exp(49) ≈ E₀ × 1.9 × 10²¹
The catastrophic escalation becomes apparent: improving from 5-sigma to 7-sigma confidence requires approximately 26 million times more energy. If E₀ represents the energy consumption of a modest laboratory experiment (~10⁶ joules), then:
3-sigma analysis: ~8 × 10⁹ joules (equivalent to a few hundred homes' daily energy use)
5-sigma determination: ~7 × 10¹⁶ joules (approaching the energy content of major hurricanes)
7-sigma quantification: ~2 × 10²⁷ joules (approaching 0.0001% of the observable universe's total energy budget)
This example reveals why observations beyond 7-sigma confidence may represent a collision with cosmic energy constraints rather than merely technical challenges.
III. The Infinite Measurement Paradox: Philosophical and Physical Dimensions
The Epistemological Challenge
The Infinite Observation Paradox operates on multiple levels, creating nested constraints on scientific knowledge:
Scale Disparity: Our most advanced analyses sample an infinitesimally small fraction of cosmic reality. Even if the universe is merely very large rather than infinite, our observational capabilities become vanishingly small in scope. The observable universe spans approximately 93 billion light-years in diameter, yet this may represent only a minuscule fraction of total cosmic reality.
Thermal Limits: Perfect quantification would require infinite energy, violating fundamental thermodynamic principles. As Brillouin demonstrated in 1953, changing an information bit value requires at least kT ln(2) energy - the same energy as Szilard's engine produces in the idealistic case.
Quantum Observation Problem: Every analysis necessarily disturbs the system being studied, creating fundamental circularity in our attempts to know objective reality. We use the universe to examine the universe, but every observation inevitably alters what we seek to understand.
The Convergence Problem
These philosophical challenges converge with practical limitations. Recent research confirms that "the preparation of the system for encoding and measuring information constrains the ability to distinguish among states of the resulting ensemble and influences the purity of these states." This creates a fundamental trade-off between analytical exactness and the energetic cost of achieving that specificity.
IV. Evidence for the Precision Horizon: Why This Synthesis is Novel
Existing Theoretical Infrastructure
Our research reveals that substantial foundational work exists across multiple disciplines, yet the specific synthesis we propose appears genuinely novel:
Thermodynamics of Observational Accuracy: Advanced dramatically through recent work establishing mathematical bounds linking analytical fidelity to thermodynamic work requirements. The quantum Fisher information framework provides rigorous connections between exactness bounds and coherence costs.
Cosmic Computational Limits: Mathematically established through Seth Lloyd's framework quantifying the observable universe's computational capacity at exactly 10^120 elementary operations using ~10^69 joules.
Interdisciplinary Bridges: Actively developing through John Wheeler's "it from bit" program, David Wolpert's stochastic thermodynamics of computation, and experimental work demonstrating thermodynamic uncertainty relations.
The Missing Connection
However, the exponential scaling relationship E ∝ exp(σ²) connecting energy costs to sigma confidence levels does not appear in current literature. While observational accuracy-energy trade-offs are well-studied, they typically involve linear relationships in thermodynamic uncertainty relations or power-law scaling in quantum metrology contexts. No existing work explicitly connects standard statistical confidence intervals to exponential energy scaling laws.
This represents the crucial missing piece that transforms isolated theoretical insights into a unified framework with practical implications for the future of accuracy science.
V. Practical Implications: The Dead End of Extreme Statistical Confidence
The Diminishing Returns Problem
Our analysis suggests that the scientific community's current trajectory toward ever-higher statistical confidence represents a fundamental misunderstanding of thermal constraints. The exponential energy scaling reveals several critical insights:
Practical technologies emerged from relatively low-accuracy quantum understanding: Lasers, computers, medical imaging, and other transformative technologies required no analyses approaching current statistical limits. Most breakthrough discoveries operated comfortably within moderate confidence bounds.
Current extreme confidence pursuits (7+ sigma, future colliders) face exponentially escalating costs: Each incremental improvement in statistical certainty demands exponentially more power, approaching cosmic-scale resource requirements. The Large Hadron Collider already consumes energy equivalent to a small city - future facilities may require energy budgets comparable to entire nations.
Practical returns diminish rapidly: The technological and scientific benefits of extreme statistical confidence do not justify the exponential power costs required to achieve them. Resources invested in pushing single experiments to 8-sigma confidence could instead fund hundreds of moderate-accuracy studies across diverse scientific domains.
The Recognition Gap
The physics community has not adequately acknowledged these thermal limits. The persistent assumption that "more energy will always buy more useful accuracy" fails to recognize that we are approaching fundamental constraints rather than merely technical challenges.
This suggests a paradigm shift toward thermodynamically informed accuracy science: working at statistical confidence levels that provide useful technology and practical results while accepting that pushing beyond certain thresholds becomes wasteful and ultimately futile.
VI. Counter-Arguments and Responses
Scientific Realism and Cumulative Progress
Critics might argue that the remarkable predictive success of scientific theories suggests they capture real features of the world's structure, making statistical improvements inherently valuable. The cumulative nature of scientific progress, where major methods and instruments are rarely completely abandoned, supports continued accuracy advancement.
Response: We do not dispute that scientific theories capture real patterns within their domains of applicability. Our argument concerns the marginal value of extreme statistical improvements versus their exponential energy costs. Scientific progress can continue productively within thermodynamically reasonable confidence bounds.
The Local Validity Argument
Defenders of extreme statistical confidence might argue that even if the universe is infinite, our local scientific laws appear remarkably consistent, suggesting that high-accuracy analyses reveal genuine features of reality's structure.
Response: Local validity remains compatible with accuracy horizons. Our framework suggests that sufficient statistical confidence for discovering local physical laws can be achieved within reasonable energy budgets, while excessive confidence beyond practical thresholds becomes thermodynamically prohibitive without corresponding gains in understanding.
Technological Spin-offs
Historical precedent shows that accuracy improvements often lead to unexpected technological breakthroughs, suggesting that apparent "dead ends" may yield unforeseen benefits.
Response: This argument fails to account for opportunity costs. The exponential energy requirements of extreme statistical confidence mean that equivalent resources could generate far greater technological benefits if invested in moderate-accuracy research across broader scientific domains.
VII. The Precision Horizon as Natural Law
A New Physical Principle
We propose that the accuracy horizon represents a fundamental physical principle comparable to other universal limits like the speed of light or the uncertainty principle. Just as relativity revealed absolute speed limits and quantum mechanics revealed absolute exactness limits for complementary variables, the precision-energy scaling law reveals absolute limits for statistical confidence in observation.
The Accuracy Horizon Principle: In any finite energy system, there exists a maximum achievable statistical confidence level σ_max beyond which observation becomes thermodynamically impossible, governed by the exponential scaling relationship between statistical requirements and energy costs.
Empirical Predictions
This principle generates testable predictions:
Energy scaling observations: Direct assessment of energy costs for achieving different sigma levels in controlled systems should reveal exponential scaling relationships.
Technological development patterns: Future accuracy technologies should show diminishing returns consistent with approaching thermal limits.
Cosmic statistical limits: Analyses requiring energy approaching significant fractions of cosmic energy budgets should become impossible regardless of technological advancement.
VIII. Conclusion: Embracing Bounded Realism
The Infinite Observation Paradox and the precision-energy scaling law together suggest a mature response to the limits of scientific knowledge. Rather than viewing these constraints as obstacles to overcome, we should recognize them as fundamental features of the cosmos that inform optimal scientific strategy.
Bounded Realism as Scientific Philosophy
We propose bounded realism as the appropriate philosophical stance: our observations and theories capture real features of the world within their proper domains, while acknowledging vast expanses of cosmic reality that may forever exceed our analytical grasp. Our 7-sigma statistical confidence represents not futile approximation but remarkable success in understanding our local cosmic neighborhood.
Strategic Implications for Science
Recognition of accuracy horizons suggests several strategic priorities:
Focus on thermodynamically efficient statistical confidence: Pursue accuracy improvements that provide maximum scientific value per unit energy investment.
Diversify rather than intensify: Instead of pushing single analyses to extreme statistical confidence, spread resources across broader scientific domains at moderate confidence levels.
Develop precision-energy analysis: Systematically evaluate the thermodynamic costs of proposed accuracy improvements before committing resources.
The Productive Paradox
The Infinite Observation Paradox serves as valuable philosophical skepticism that illuminates important limitations while avoiding pessimistic overreach. Yes, our analyses are finite in a potentially infinite cosmos, and this should induce intellectual humility about the scope of scientific knowledge. However, the cumulative success of science within reasonable confidence bounds suggests we are discovering meaningful local regularities.
The universe may indeed be much larger than we can comprehend, but our finite observations in our finite analytical domain constitute genuine knowledge about the structure of reality - even if that reality extends infinitely beyond our instruments. The accuracy horizon does not limit scientific knowledge itself, but rather guides us toward thermodynamically sustainable scientific practice.
The paradox reminds us that even our greatest scientific achievements operate within fundamental limits - thermal, informational, and observational. This recognition should foster both wonder at what we have achieved and wisdom about how to direct our finite energetic resources toward the most productive scientific endeavors.
In embracing the accuracy horizon, we embrace a more mature relationship with the cosmos: one that recognizes both our remarkable capabilities and our fundamental constraints, guiding us toward a sustainable future for statistical science within the thermodynamic realities of our finite universe.
This essay represents a novel synthesis of established principles from information theory, quantum thermodynamics, and cosmological physics. The proposed precision-energy scaling law σ_max = f(E_universe, k_B T, measurement_efficiency) awaits empirical validation but provides a framework for understanding fundamental limits to observational accuracy that may inform the future development of statistical science.
References and Citations
LIGO Laboratory Facts - https://www.ligo.caltech.edu/page/facts
LIGO Detection Capabilities - https://en.wikipedia.org/wiki/LIGO
MIT News: Gravitational Waves Detection - https://news.mit.edu/2016/ligo-first-detection-gravitational-waves-0211
Physics World: Fundamental Constants Precision - https://physicsworld.com/a/fundamental-constant-measured-at-highest-precision-yet/
National Science Review: Precision Measurement Physics - https://academic.oup.com/nsr/article/3/4/457/2669369
Cosmic Distance Ladder - https://en.wikipedia.org/wiki/Cosmic_distance_ladder
Stellar Parallax Methods - https://www.vaia.com/en-us/explanations/physics/astrophysics/stellar-distances/
Astronomy Distance Measurements - https://astronomy.com/magazine/greatest-mysteries/2019/07/the-cosmic-distance-ladder
Observable Universe Scale - https://en.wikipedia.org/wiki/Observable_universe
Universe Infinity Discussion - https://bigthink.com/starts-with-a-bang/universe-infinite/
Quantum Observer Effect - https://en.wikipedia.org/wiki/Observer_effect_(physics)
ArXiv: Incompleteness and Physics - https://arxiv.org/abs/quant-ph/0206014
Landauer's Principle - https://en.wikipedia.org/wiki/Landauer%27s_principle
Information Theory and Thermodynamics - https://en.wikipedia.org/wiki/Entropy_in_thermodynamics_and_information_theory
Stanford Encyclopedia: Scientific Realism - https://plato.stanford.edu/entries/scientific-realism/
Royal Society: Scientific Paradigms - https://royalsocietypublishing.org/doi/10.1098/rsos.191717
Penn State: Observable Universe Limits - https://www.psu.edu/news/research/story/veil-visible/
Stanford Encyclopedia: Measurement in Science - https://plato.stanford.edu/entries/measurement-science/